1.2: b
  1.3: b
  1.4: b
  1.5: a
  1.6: a
  1.7: a
  1.8: b
  1.9: a
  1.10 Coefficients 1c: b0=2
  1.11 Coefficients 1a: a1=0.24
  1.12 Problem 1 comments: We can figure out the impulse response and frequency response of given filter by using 
  Z-transform. 
  2.1: b
  2.2: c
  2.3 Coefficients 2b: b0=2, b1=-0.707
  2.4 Coefficients 2a: a1=-1.414, a2=1
  2.5 Problem 2 comments: The signal that has only one frequency can be expressed as one component in the frequency 
  domain(ideal case).
  3.1: c
  3.2: b
  3.3: a
  3.4 Coefficients: b0=1, b1=-1.414, b2=1
  3.5 Problem 3 comments: The h(n) have canceled out some of input signal that the original signal was changed.

  4.1: c
  4.2: b
  4.3: c
  4.4 Coefficients: b0=1, b1=0.5, b2=0.25, b3=0.25, b4=0.5, b5=1
  4.5 Problem 4 comments: H(z) : symmetric ----> Phase Response : constant slope 
  5.1: a
  5.2: a
  5.3: a
  5.4: a
  5.5: c
  5.6 Problem 5 comments: There can be more than one H(z) with same response. The poles at near w=0 can make the filter 
  gain higher near low 
  frequency. The zeros at near w=pi can make the filter gain lower near high frequency.
  6.1: a
  6.2: b
  6.3: a
  6.4: c
  6.5: b
  6.6: a
  6.7: c
  6.8 Problem 6 comments: y = x*h = x*(h1*h2) = (x*h1)*h2 y = x*h = x*(h1+h2) = (x*h1)+(x*h2)
 

Graph 1

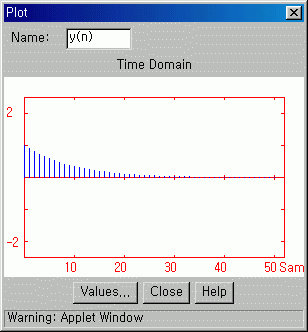
Graph 2

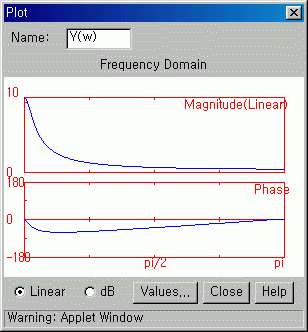
Graph 3

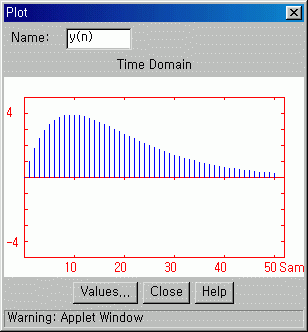
Graph 4

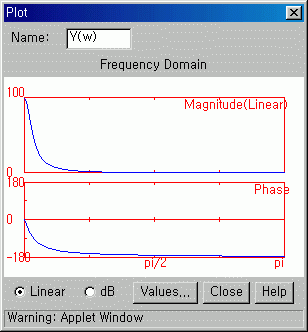
Graph 5