|
A
method of protein secondary structural classification is proposed. This method
uses the mean of the linear prediction derived cepstral feature vectors of
protein sequences numerically mapped using two different existing amino acid
indexing techniques, namely EIIP and Oobatake-Ooi indexing. The classifier’s
performance is evaluated using the resubstitution test, the jackknife test, and
the 10-way CV method. It demonstrates a 3% improvement (both for jackknife and
resubstitution) over the ACF approach and an 8% (jackknife) and 6% (resubstitution)
improvement over the component coupled algorithm which is an AAC approach. The
robustness of the proposed classifier is tested. The existing computational
approaches for protein structural classification using the 20 normalized
frequencies derived from AAC are based on this principle. However, the
classifiers primarily using AAC firstly do not have a unique one-to-one mapping
between the primary sequence and the normalized frequency vector. Secondly,
these methods do not capture similarities in the sequences’ resonant recognition
model (RRM) spectra, and other physicochemical properties. These inadequacies
can be solved by replacing the AAC based frequency vectors by spectral feature
vectors. The spectral features have a unique mapping with the numerically mapped
primary sequence and they have been found to exhibit better capabilities in
capturing the global similarities between sequences
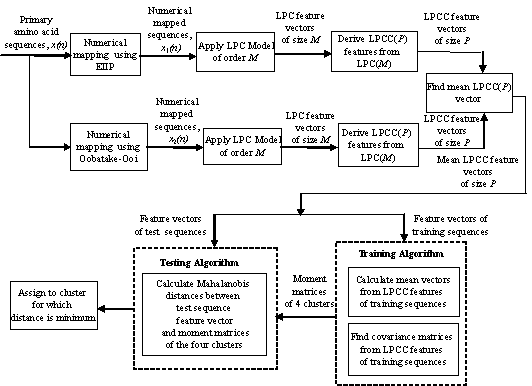
Figure 1. Block Diagram of the Proposed Classifier.
The cepstral coefficients are the coefficients of the Fourier
transform representation of the logarithm magnitude squared spectrum of the
numerical amino acid sequence. The cepstral coefficients obtained by this method
represent the fine structure of the amino acid sequence spectrum which is not
very useful for pattern classification problems [11] whereas the LP based
cepstral coefficients (LPCC) retain only the smoothed spectral behavior
(spectral envelope) of the numerically mapped amino acid sequence and hence,
serve as a useful tool for pattern classification. These can be derived from the
LPC using a recursion formula. The number of cepstral coefficients, L (>=p). The
selection of the order of linear prediction p plays a pivotal role in the
performance of the clustering algorithm. It varies with the length of the amino
acid sequences and also with the size of the datasets used. In our algorithm, we
have used L=p in all cases, because the performance of the classifier doesn’t
change on increasing L more than p.The proposed algorithm uses the equally
weighted mean of the cepstral feature vectors obtained from each sequence mapped
using the two indexing techniques, as the final feature vector.
We use the Mahalanobis distance
metric. There are four clusters, corresponding to the four structural classes of
proteins, into which the test sequences are classified. The LxL
covariance matrix for each cluster is made up of normalized covariances between
the NtxL cepstral coefficients, Nt is
the number of training sequences in cluster t where t = α, β, α+β,
α/β.
|
 |
 |
|
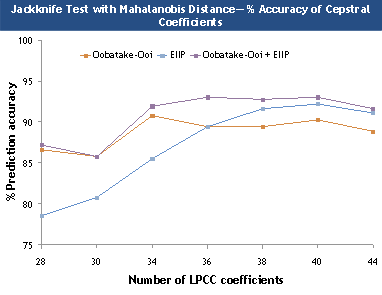
Figure 2. Overall prediction accuracies for jackknife test
using the three indexing techniques.
|
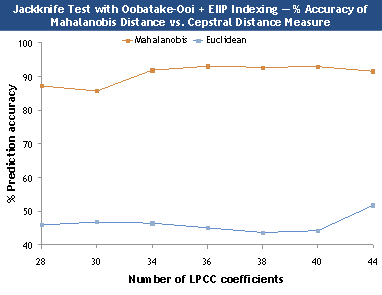
Figure 3. Comparison between Mahalanobis and cepstral
distance measure.
|
The dataset used here consists of 359 proteins extracted from
structural class of proteins (SCOP) database. We have used the same dataset used
by authors in the component coupled algorithm and the ACF. We use three tests
namely, resubstitution test, jackknife test, and the 10-way cross-validation
(CV) test. The first two tests have been used by many authors dealing with this
problem. We have used an additional 10-way cross-validation method to obtain an
upper bound estimate of the classification error. We observe that combining
these two techniques improves the performance of the classifier. The use of
modified LPCC feature sets not only increases the overall prediction accuracy of
the classifier but also demonstrates comparable performance for all the
structural classes.
|



