J-DSP Lab
5: The Fast Fourier Transform (FFT)
Lab 5 concentrates on the Fast
Fourier Transform (FFT).
Problem 5-1: FFT Properties
Consider the symmetries in the
following signals. We want to see how these symmetries affect FFT spectra.
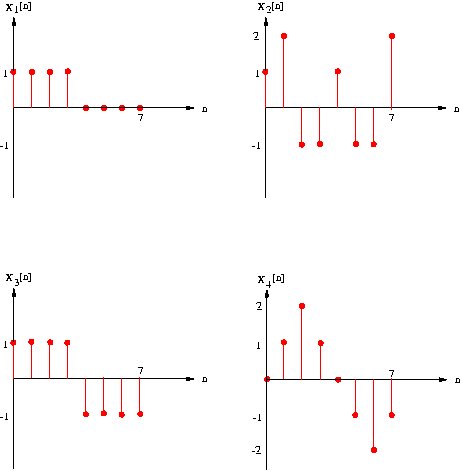
1. Generate the given signals in J-DSP and plot the FFT
of size N=8.
Note: In the Sig
Gen block dialog box, set the “signal” to Self-Defined
and an [Edit Signal] button will appear.
Click the [Edit Signal] button
and enter the index along with the desired value of the signal at that index.
Click the [update] button for the change to take effect. The new value is then shown in the table.
2. For which of these FFT plots is the real (imaginary)
part zero?
Problem 5-2: The Rectangular
Window
In this exercise we want to see
the effect of truncation on the FFT spectra.
We will subsequently try tapered windows as well. Generate a sine wave
of “gain” 1, “pulse width” 128 samples, and “time shift” 0, with ”frequency” p/10 = 0.1 p.
Window (truncate) the sine wave
for both cases below and plot the FFT of size N=128 for both cases (use dB
scaling).
i)
A rectangular
window of length 64 samples (what does this represent? zero padding?)
ii)
A rectangular
window of length 128 samples (is the sinusoid resolved exactly?)
Plot the FFT of size N=128 for
both cases (use dB scaling).
iii)
Repeat i) and ii) for “frequency” p/11.
Compare the outputs between each
of the four cases. Explain the differences in the FFT magnitude plots. Think of
the effects of the windows and zero padding; also try to figure out the
frequencies that the 128-point FFT can resolve exactly.
Problem 5-4: Window Tradeoffs
Generate the following signal
![]()
Window x(n)
with
i)
A rectangular
window of length 128
ii)
A Hamming window
of length 128
Using J-DSP, plot the FFT of
size N=128 for both cases (use dB scaling).
Why is the shape of the FFT different?
Which window would you choose and why?